Module 4 - Data Visualization

library(tidyverse)

Basics

Modify the code below to make the points larger triangles and slightly transparent. See ?geom_point for more information on the point layer.

ggplot(mpg) + 
  geom_point(aes(x = displ, y = hwy))

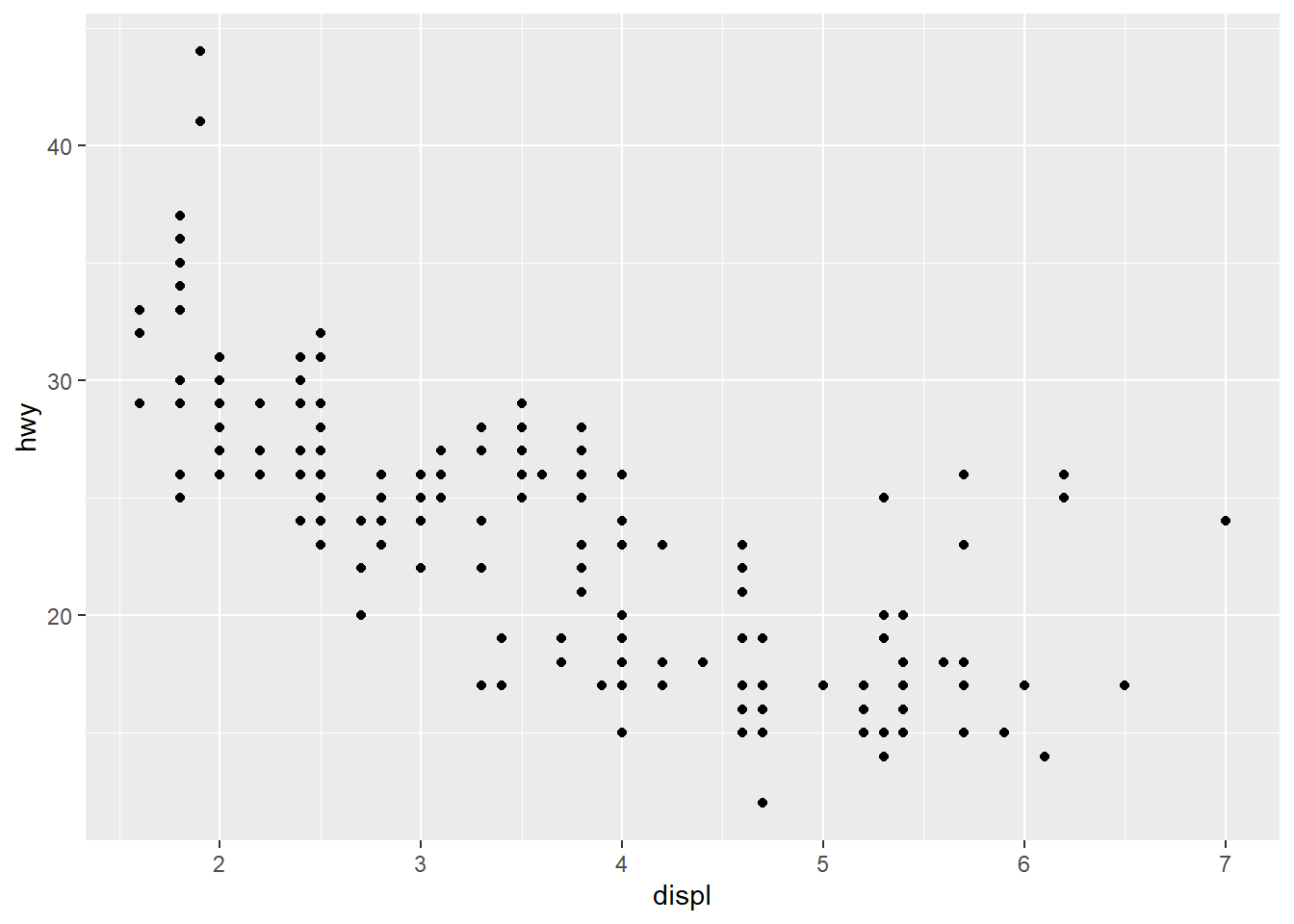
Solution:

ggplot(mpg) + 
  geom_point(aes(x = displ, y = hwy), shape="triangle", size=4, alpha=0.5)

---

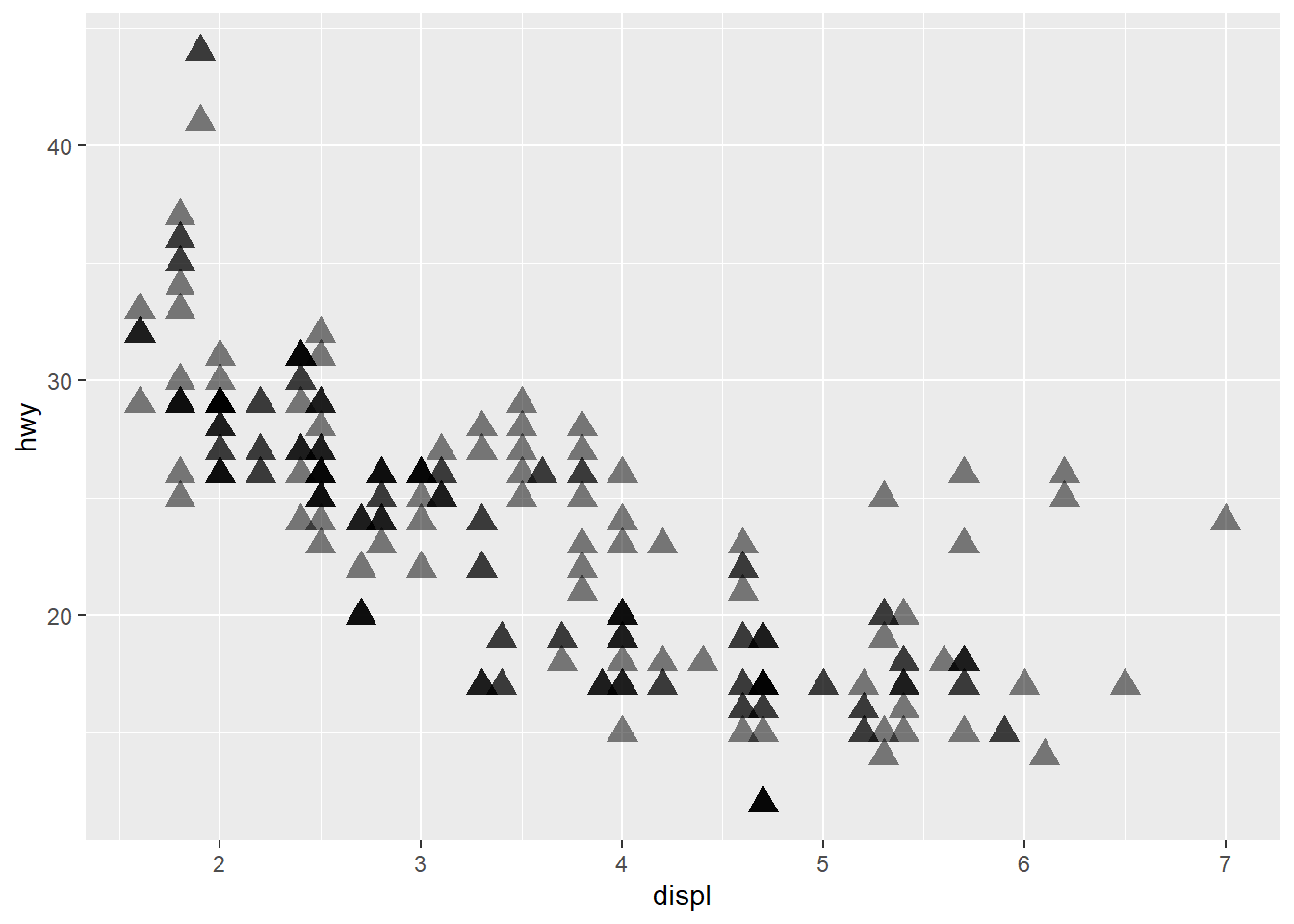
Using the mpg dataset draw a line chart, a boxplot, and a histogram

Solution:

ggplot(data=mpg)+
  geom_line(aes(x=displ, y=hwy))

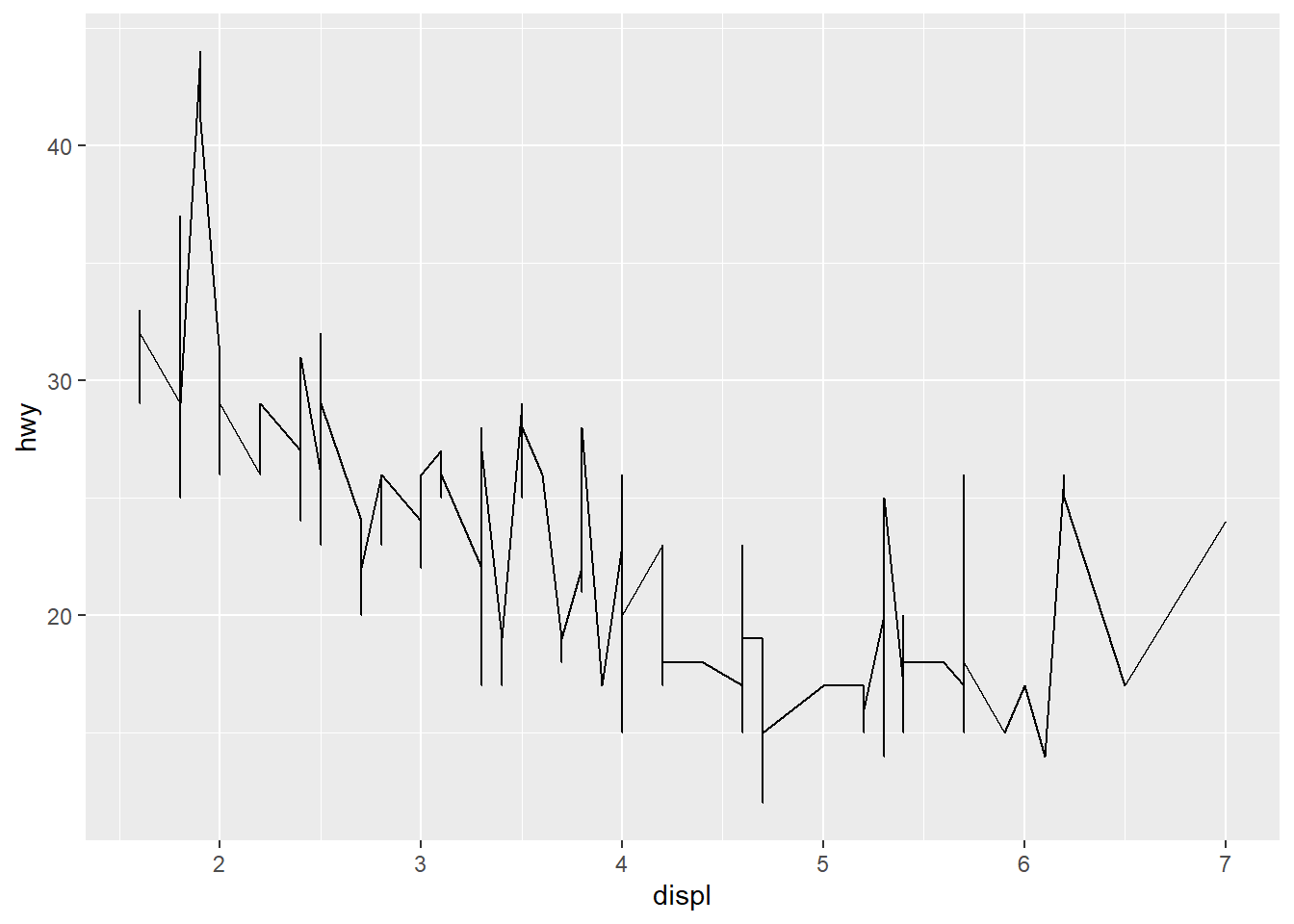
ggplot(data=mpg)+
  geom_boxplot(aes(x=class, y=displ))

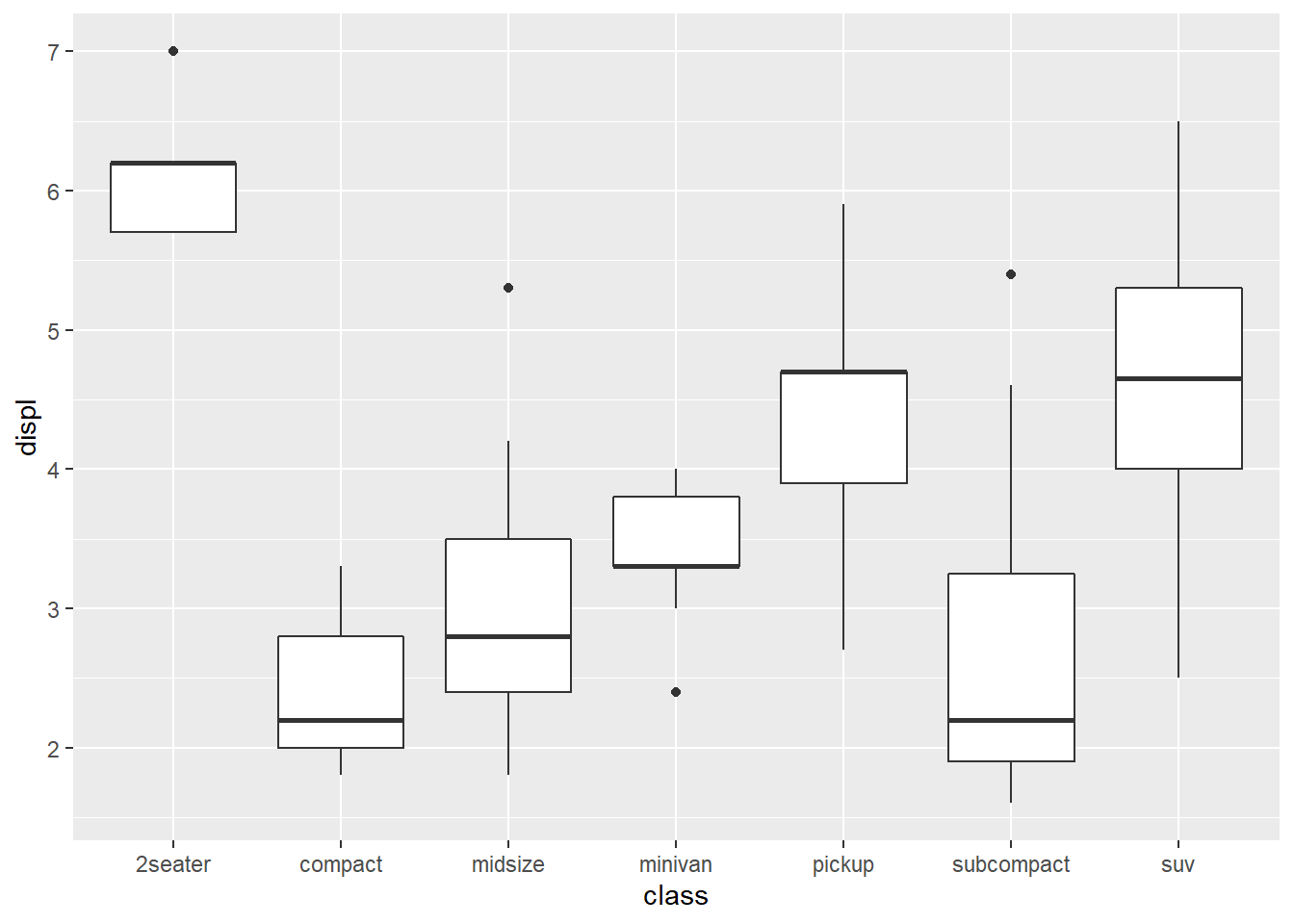
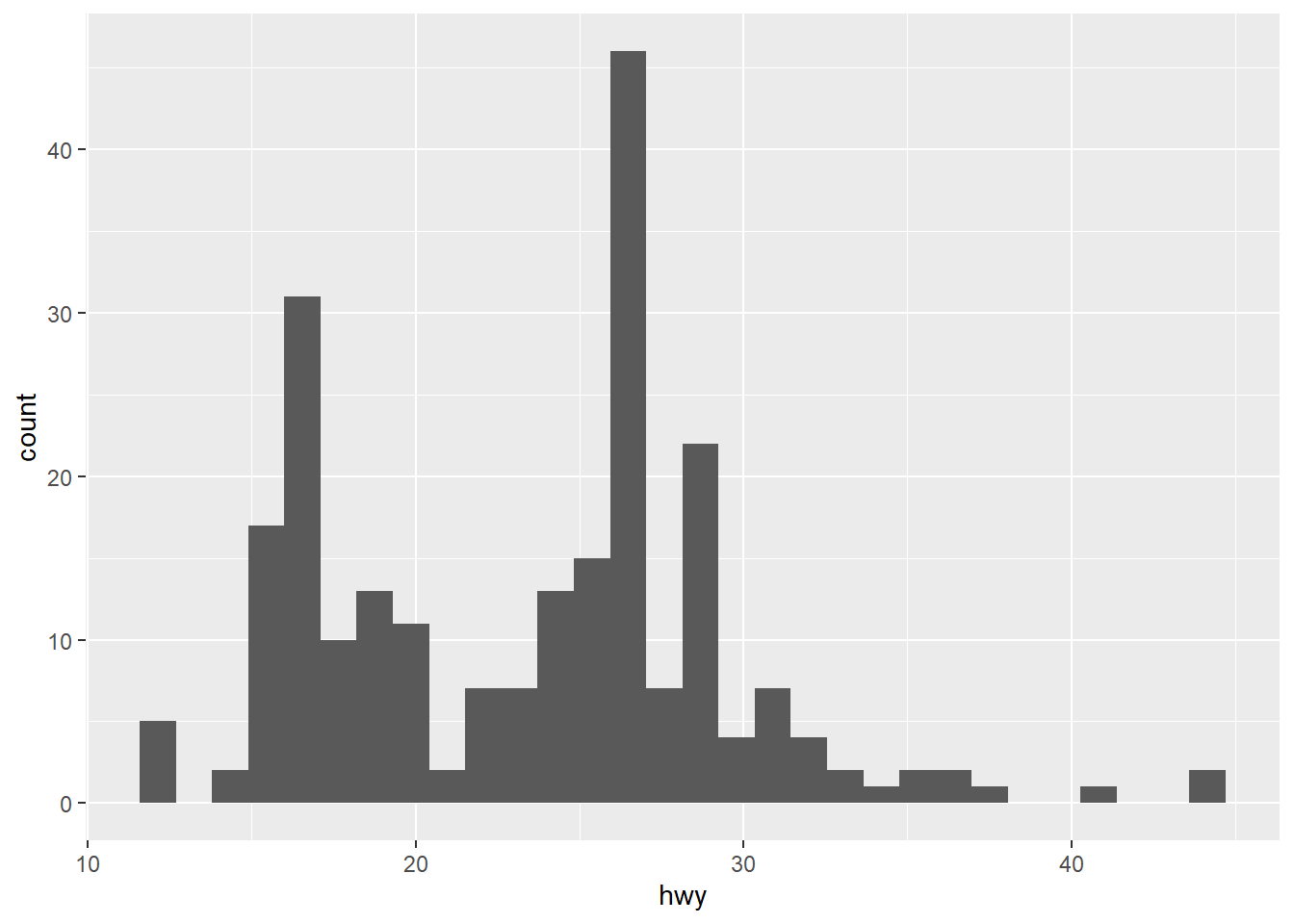
ggplot(data=mpg)+
  geom_histogram(aes(x=hwy))

## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.

Stat

What does geom_col() do? How is it different from geom_bar()?

Look at the documentation for geom_bar using ?geom_bar

---

We learnt that geom_*() and stat_*() are interchangeable. Can you look at ?geom_bar() and figure out which stat it uses as default. Modify the code below to use that stat directly instead

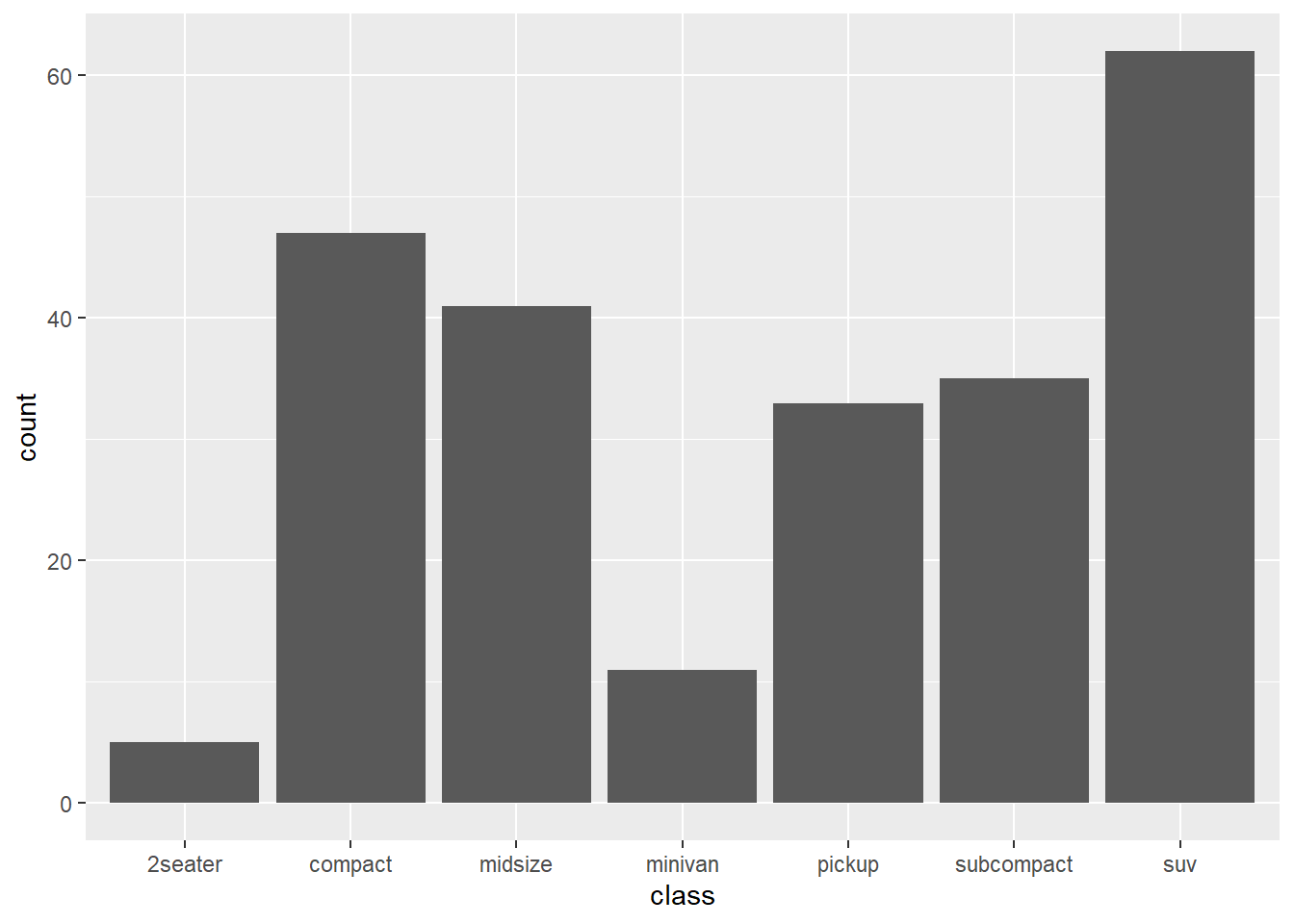
ggplot(mpg) + 
  geom_bar(aes(x = class))

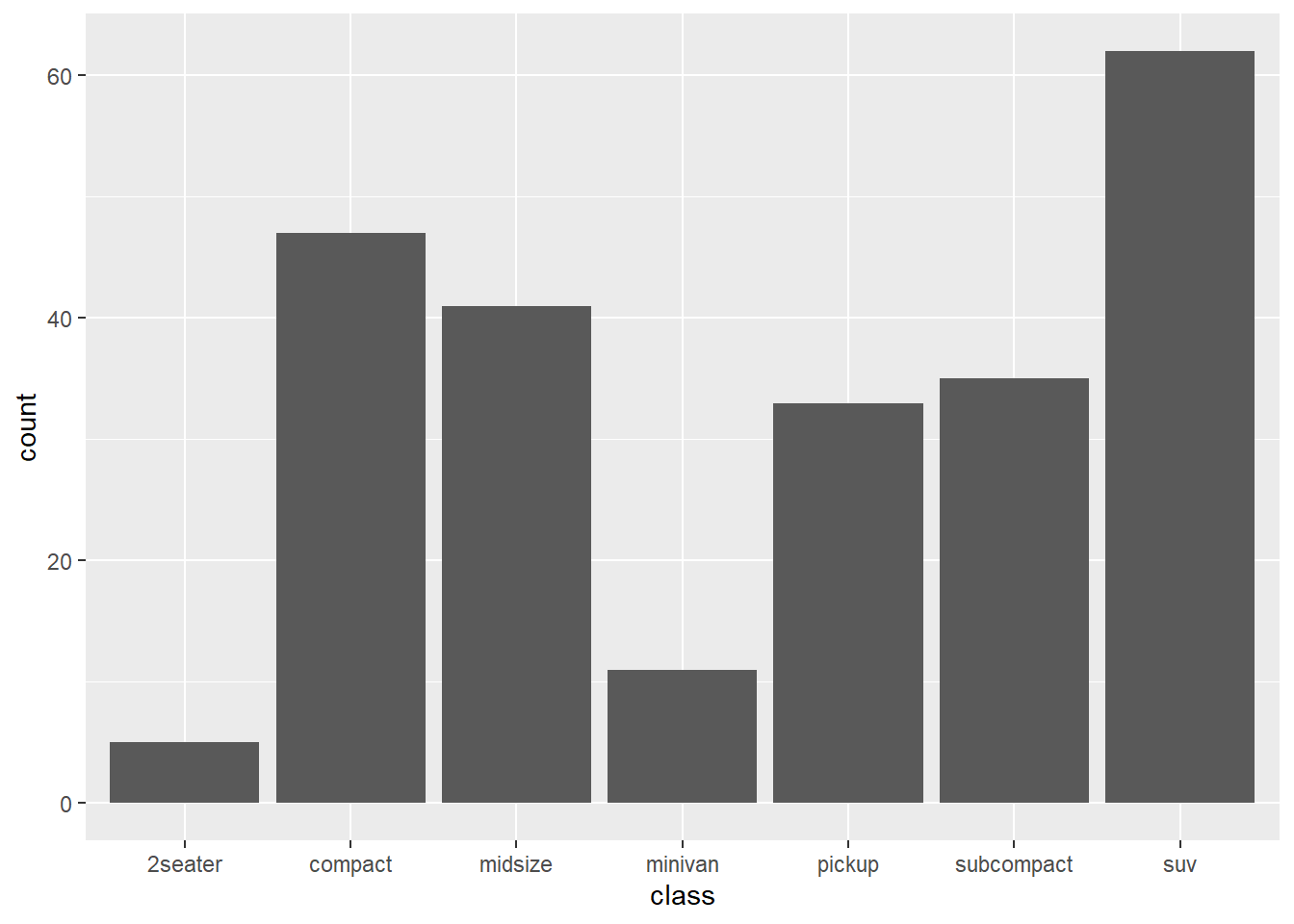
Solution: The description says “geom_bar() uses stat_count() by default”. Using it directly below:

ggplot(mpg) + 
  stat_count(aes(x = class))

---

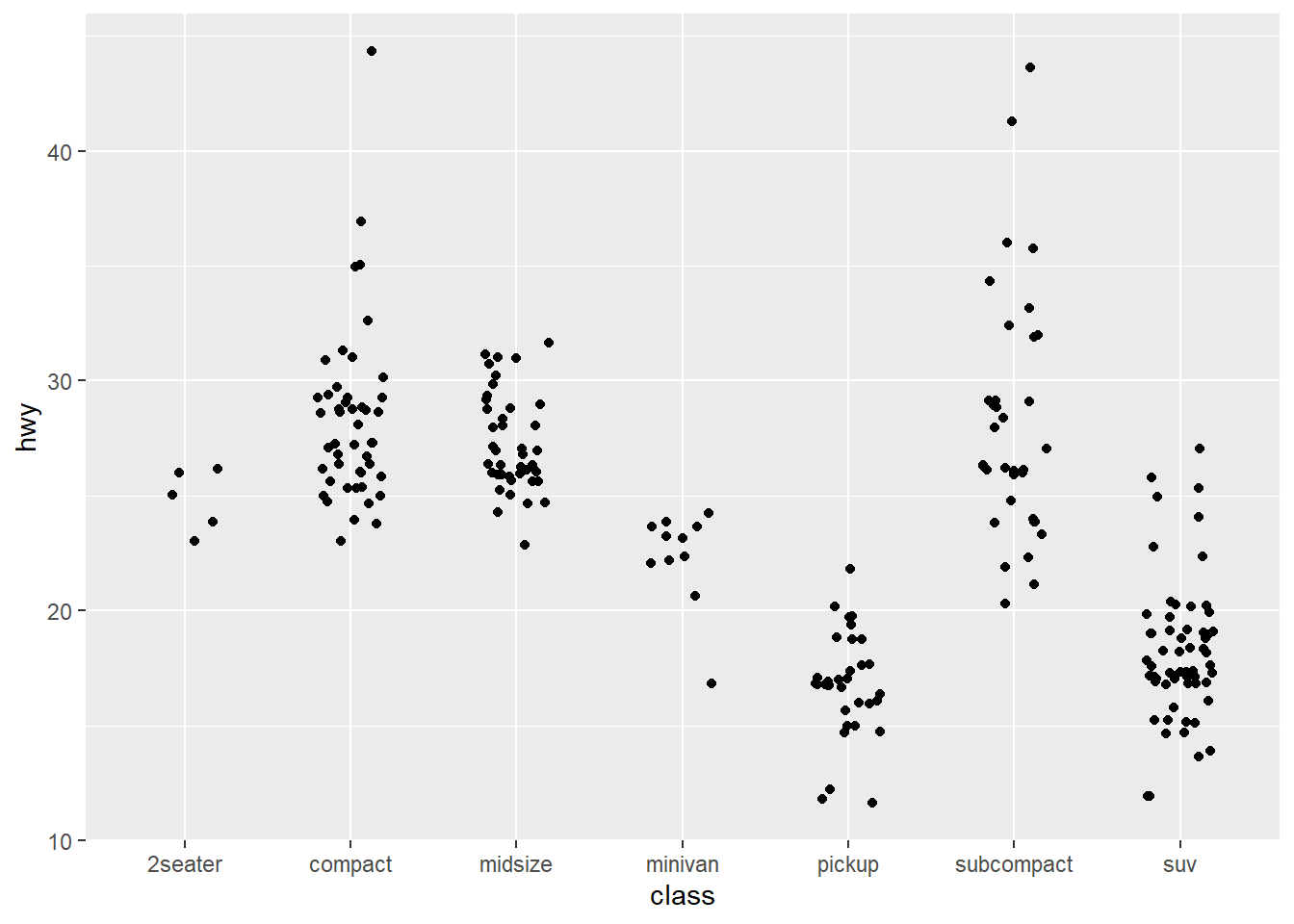
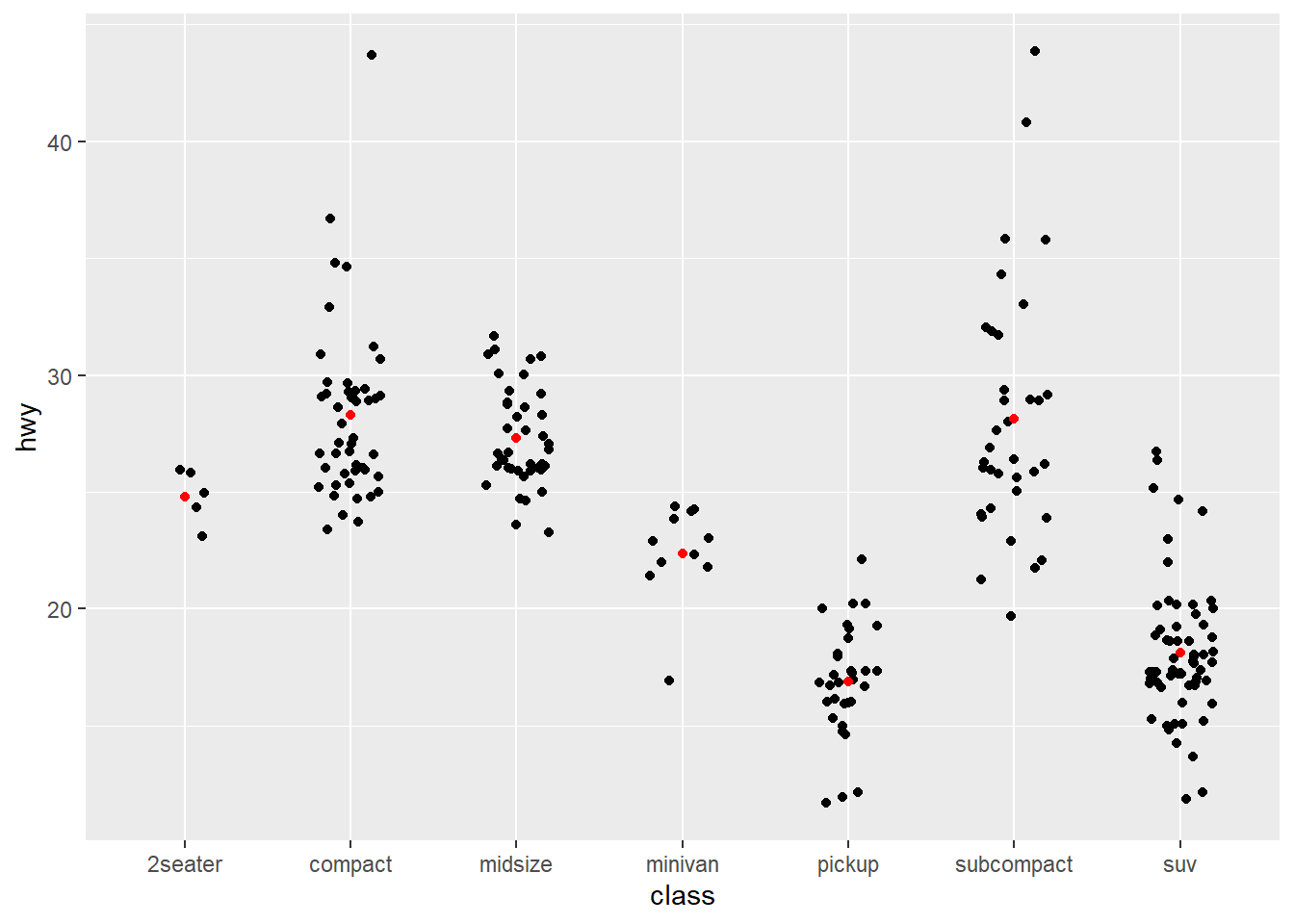
Use stat_summary() to add a red dot at the mean hwy for each group

ggplot(mpg) + 
  geom_jitter(aes(x = class, y = hwy), width = 0.2)

Hint: You will need to change the default geom of stat_summary()

Solution:

ggplot(mpg, aes(x=class, y=hwy)) + 
  geom_jitter(width = 0.2)+
  stat_summary(geom = "point", fun="mean", color="red")

---

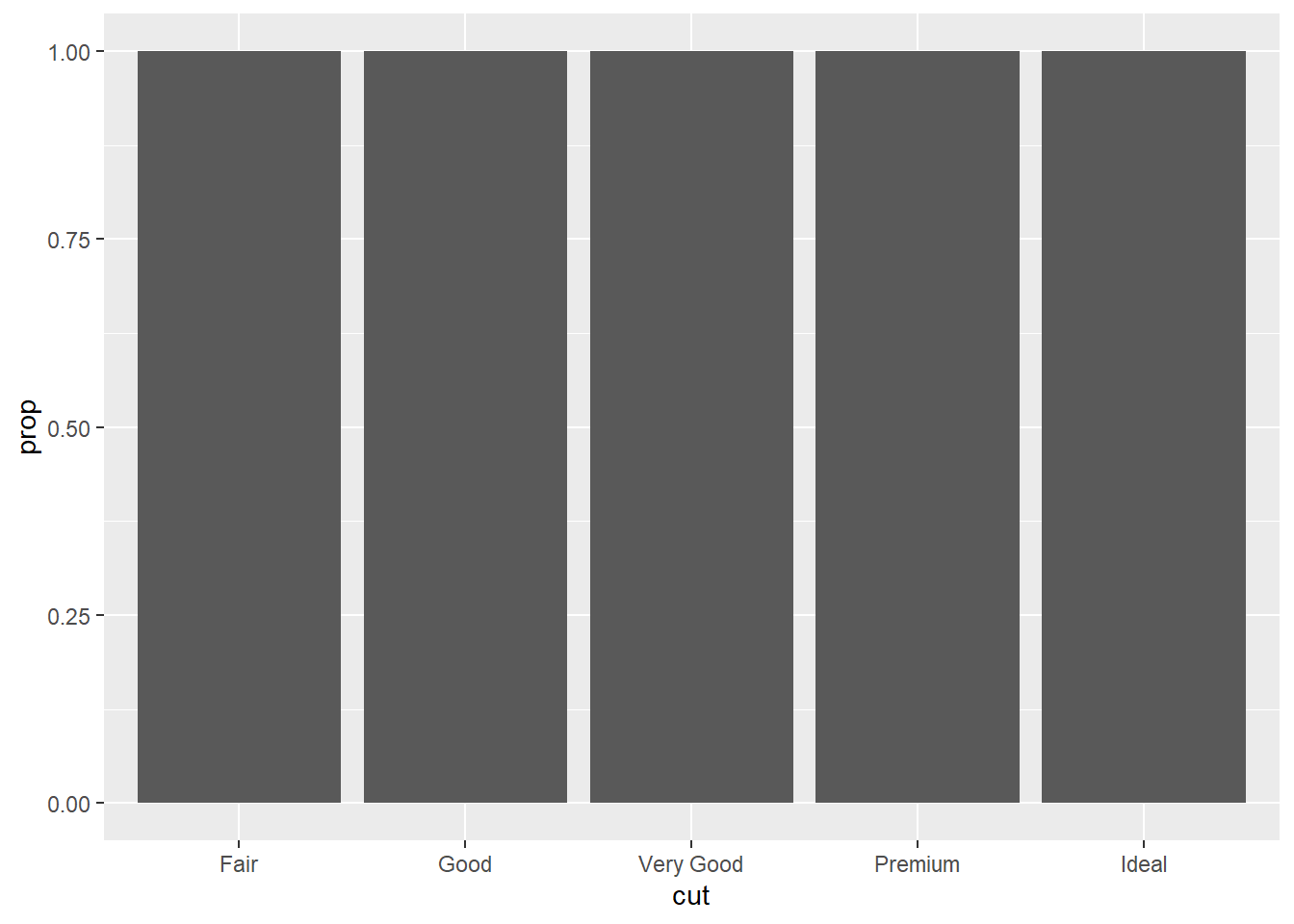
In our proportion bar chart, we need to set group = 1. Why? In other words what is the problem with these two graphs?

p1<- ggplot(data = diamonds) + 
  geom_bar(mapping = aes(x = cut, y = after_stat(prop)))

p2<-ggplot(data = diamonds) + 
  geom_bar(mapping = aes(x = cut, fill = color, y = after_stat(prop)))

p1

p2

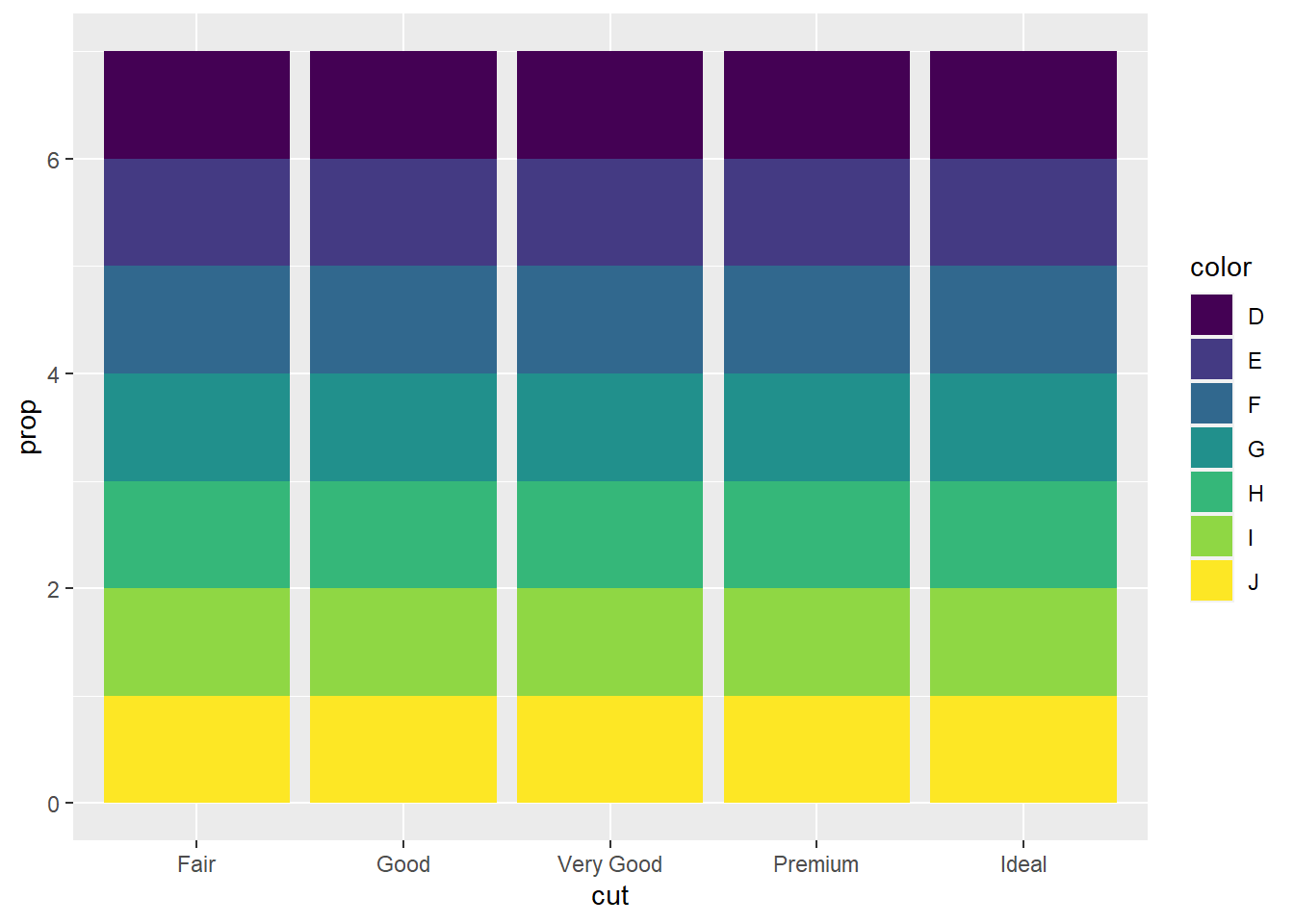
Solution: if group = 1 is not included, the proportions will be calculated within each group. Modified code is below.

p1_new<- ggplot(data = diamonds) + 
  geom_bar(mapping = aes(x = cut, y = after_stat(prop), group=1))

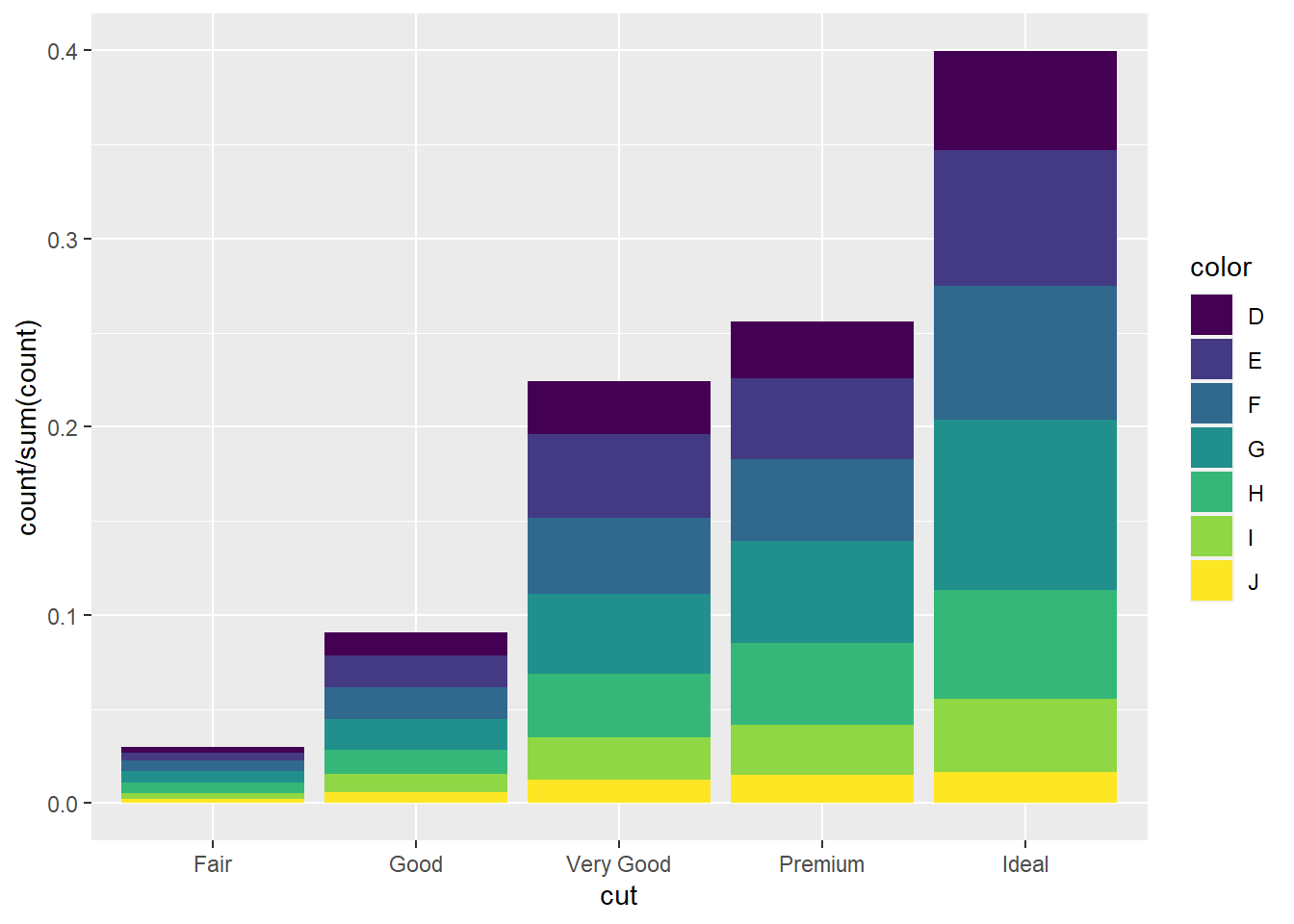
p2_new<-ggplot(data = diamonds) + 
  geom_bar(mapping = aes(x = cut, fill = color, y = ..count.. / sum(..count..)))

p1_new

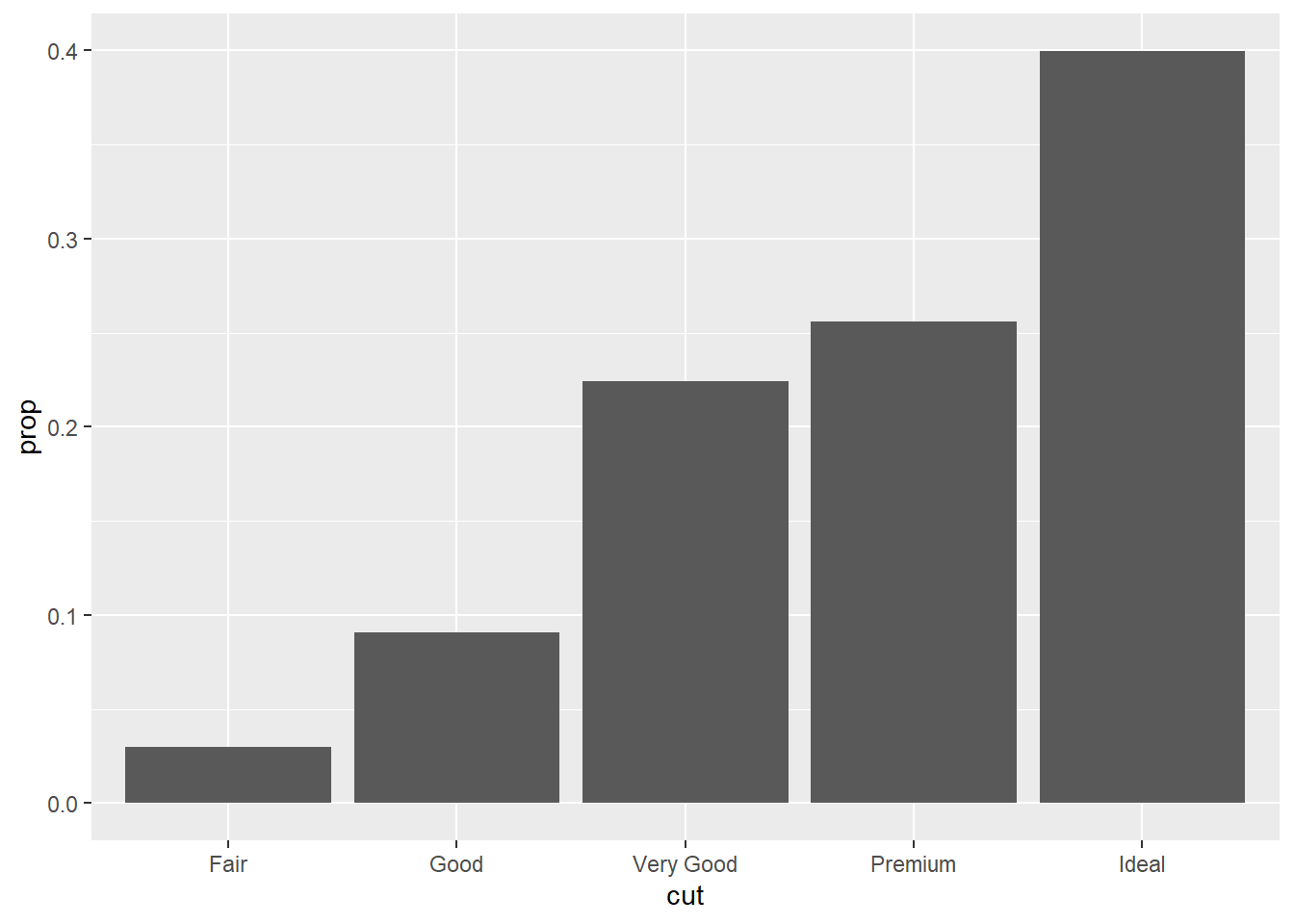
p2_new

*** What is the problem with this plot? How could we improve it?

ggplot(data = mpg, mapping = aes(x = cty, y = hwy)) + 
  geom_point( )

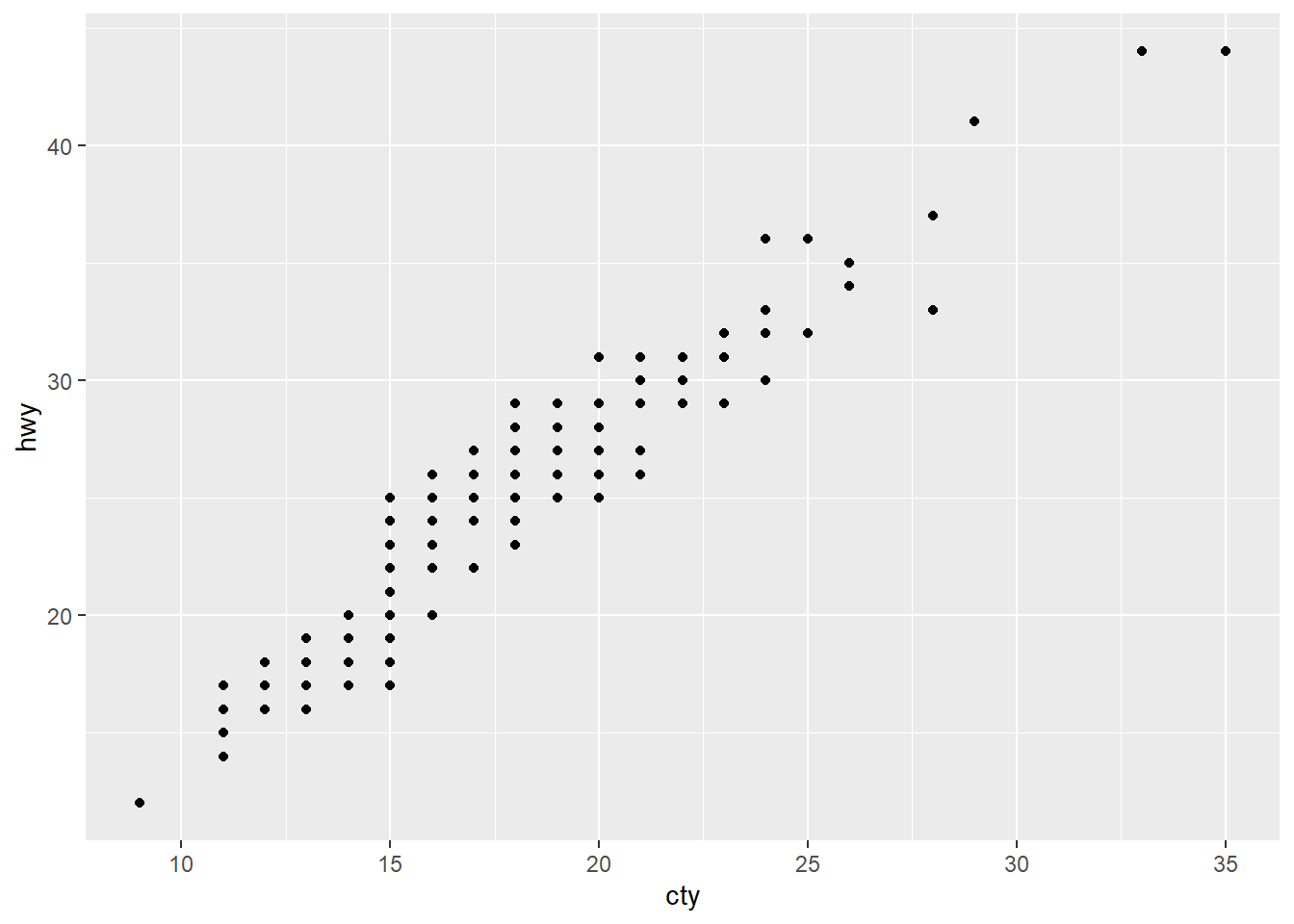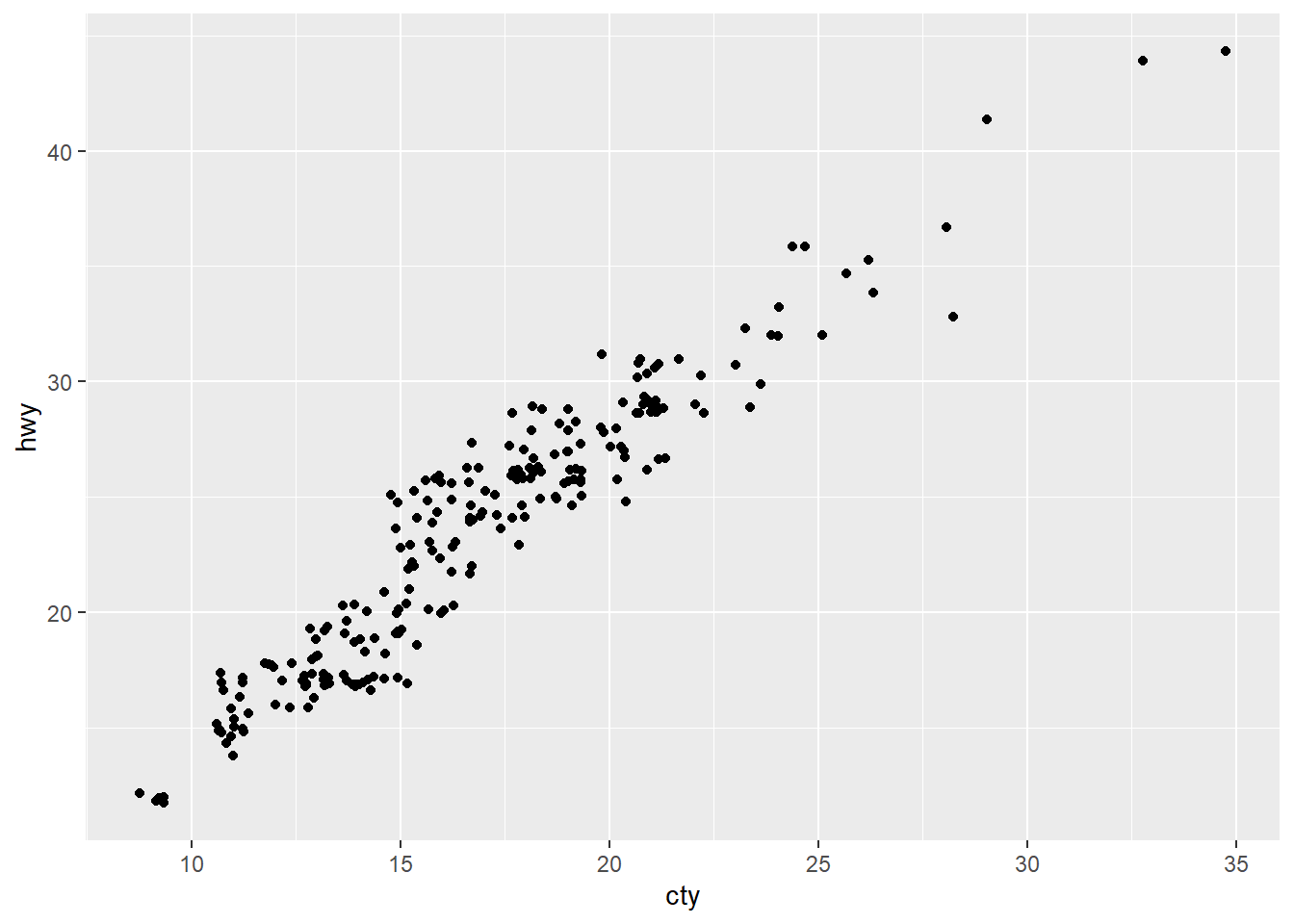
Solution: There is overplotting because there are multiple observations for each combination of cty and hwy values.

ggplot(data = mpg, mapping = aes(x = cty, y = hwy)) + 
  geom_point(position="jitter" )

Scales

Use RColorBrewer::display.brewer.all() to see all the different palettes from Color Brewer and pick your favourite. Modify the code below to use it

ggplot(mpg) + 
  geom_point(aes(x = displ, y = hwy, colour = class)) + 
  scale_colour_brewer(type = 'qual')

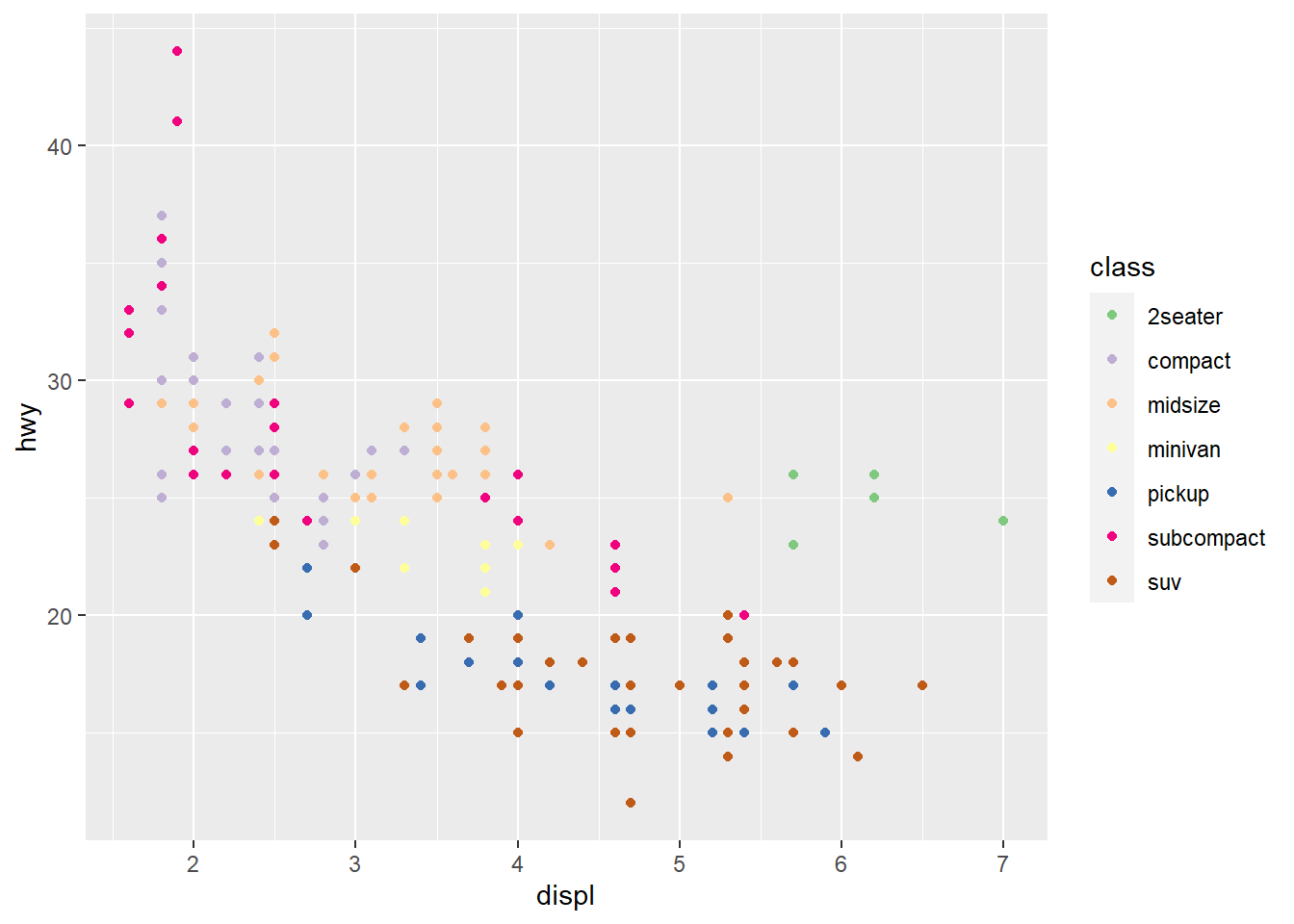
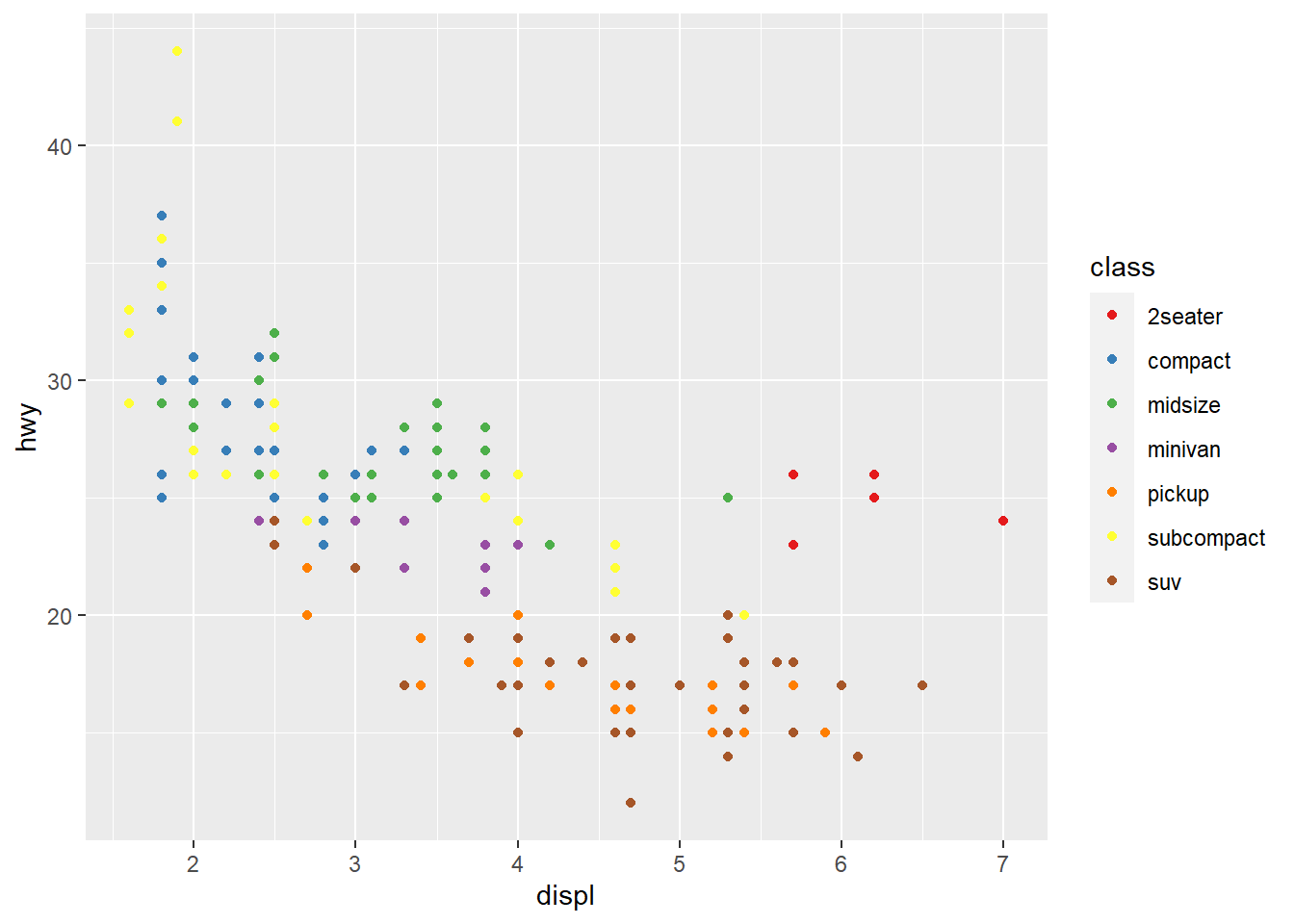
Solution:

data("mpg")
ggplot(mpg) + 
  geom_point(aes(x = displ, y = hwy, colour = class)) + 
  scale_colour_brewer(type = 'qual', palette = "Set1")

* * *

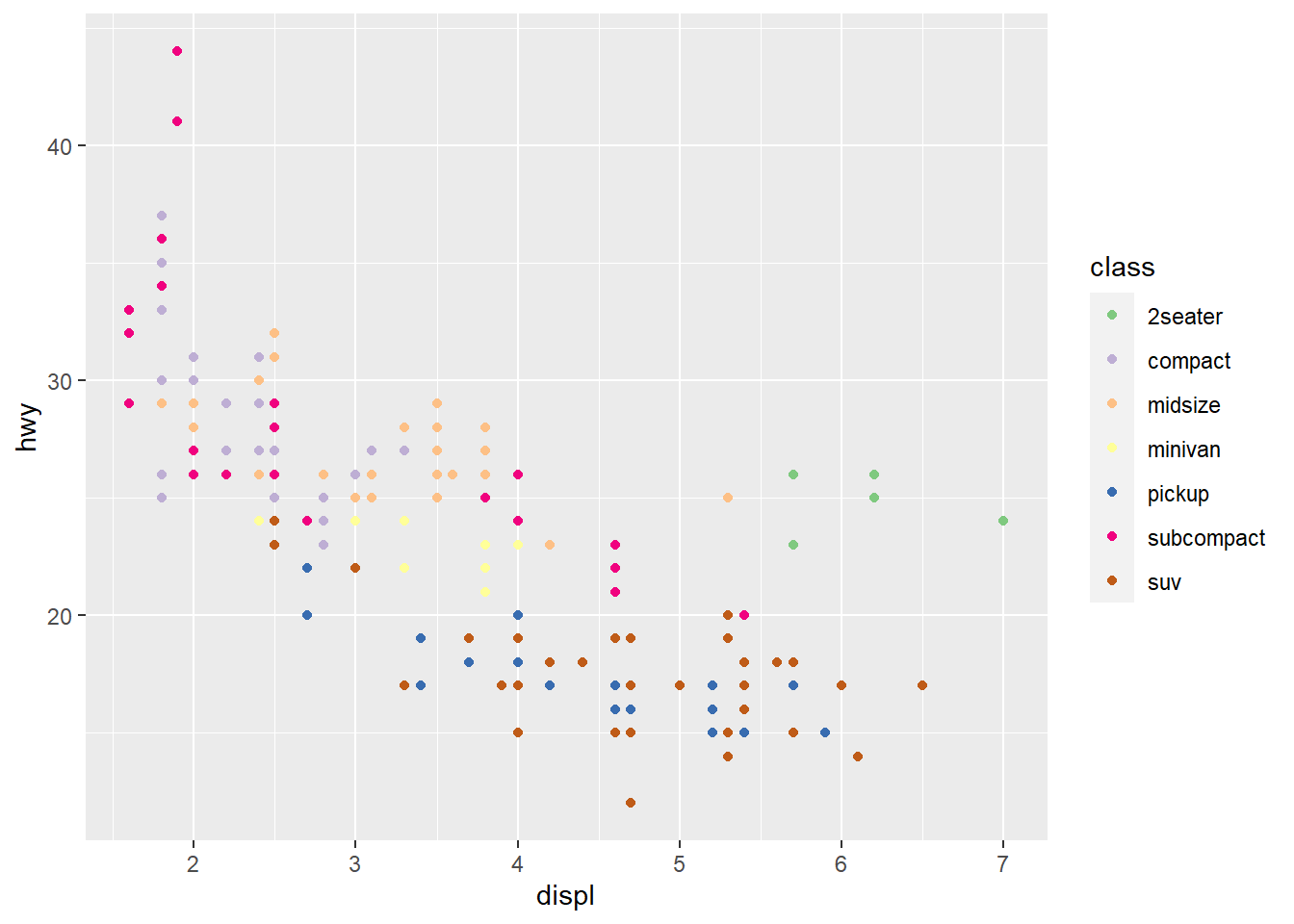
Modify the code below to create a bubble chart (scatterplot with size mapped to a continuous variable) showing cyl with size. Make sure that only the present amount of cylinders (4, 5, 6, and 8) are present in the legend.

ggplot(mpg) + 
  geom_point(aes(x = displ, y = hwy, colour = class)) + 
  scale_colour_brewer(type = 'qual')

Hint: The breaks argument in the scale is used to control which values are present in the legend.

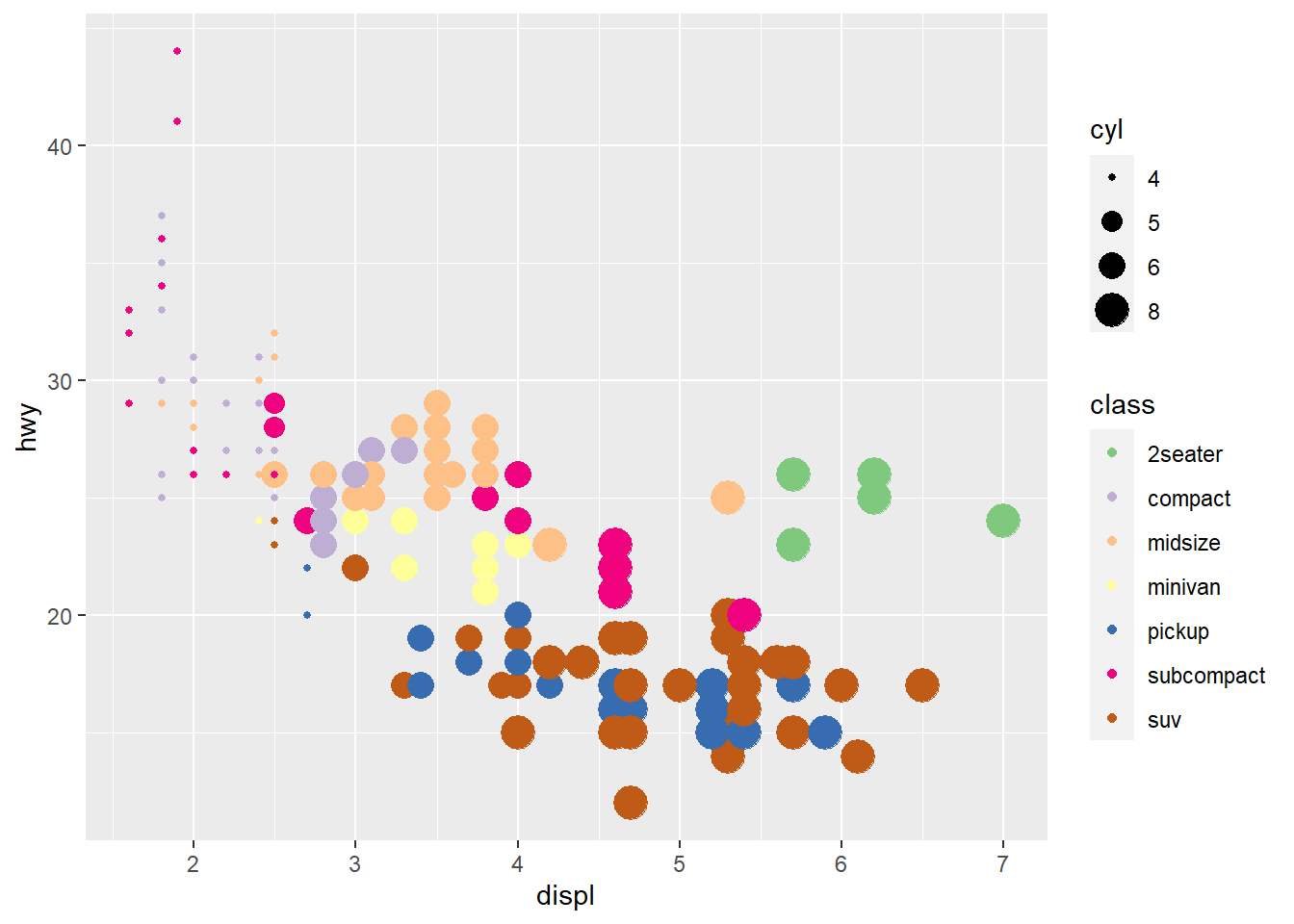
Solution:

ggplot(mpg) + 
  geom_point(aes(x = displ, y = hwy, colour = class, size=cyl)) + 
  scale_colour_brewer(type = 'qual') +
  scale_size(breaks = c(4, 5, 6, 8))

Explore the different types of size scales available in ggplot2. Is the default the most appropriate here?

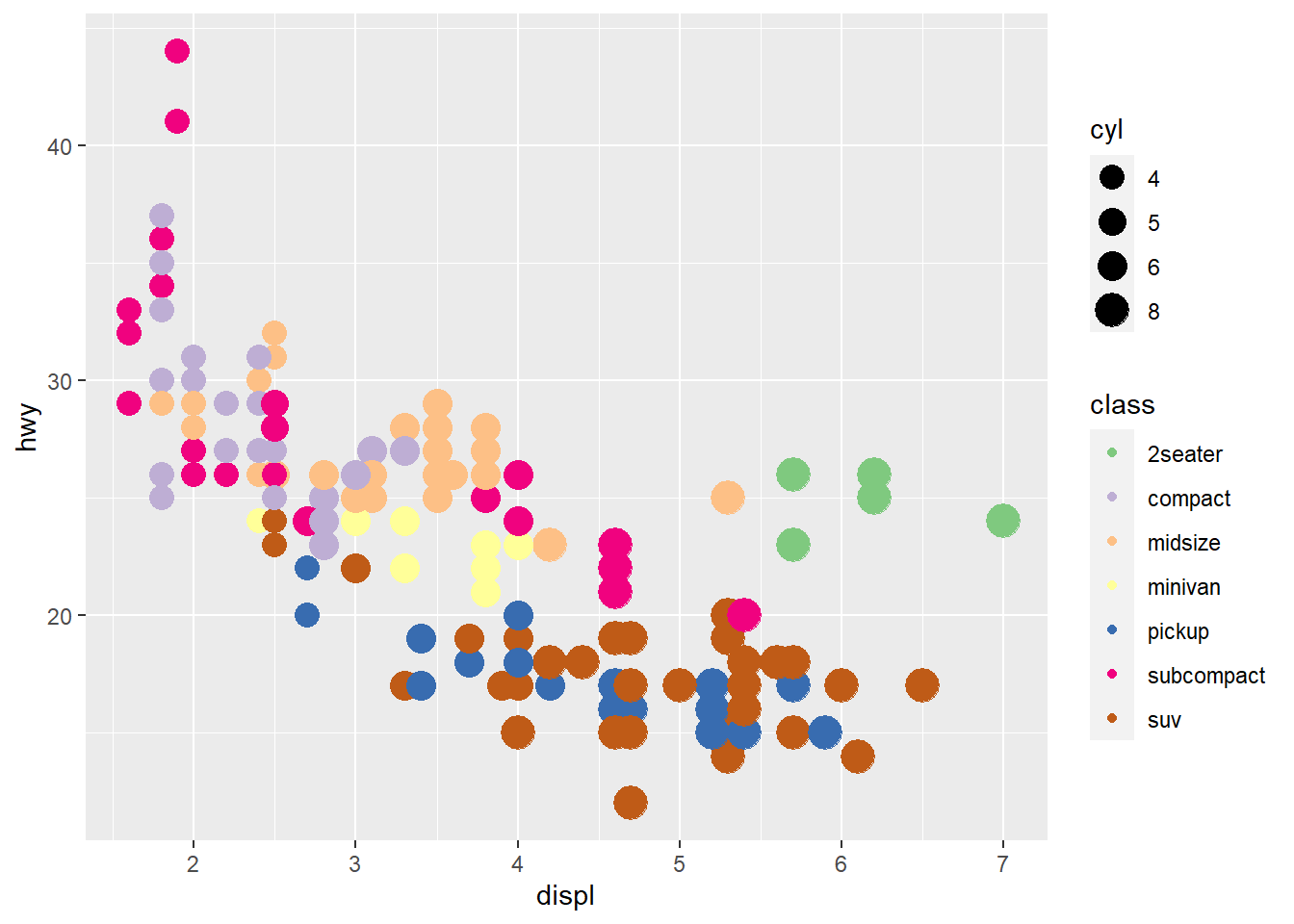
Solution: Default is mapping to the radius. But it is not intuitive. Let’s try size mapping by area.

ggplot(mpg) + 
  geom_point(aes(x = displ, y = hwy, colour = class, size=cyl)) + 
  scale_colour_brewer(type = 'qual') +
  scale_size_area(breaks = c(4, 5, 6, 8))

* * *

Modify the code below so that colour is no longer mapped to the discrete class variable, but to the continuous cty variable. What happens to the guide (legend)?

ggplot(mpg) + 
  geom_point(aes(x = displ, y = hwy, colour = class, size = cty))

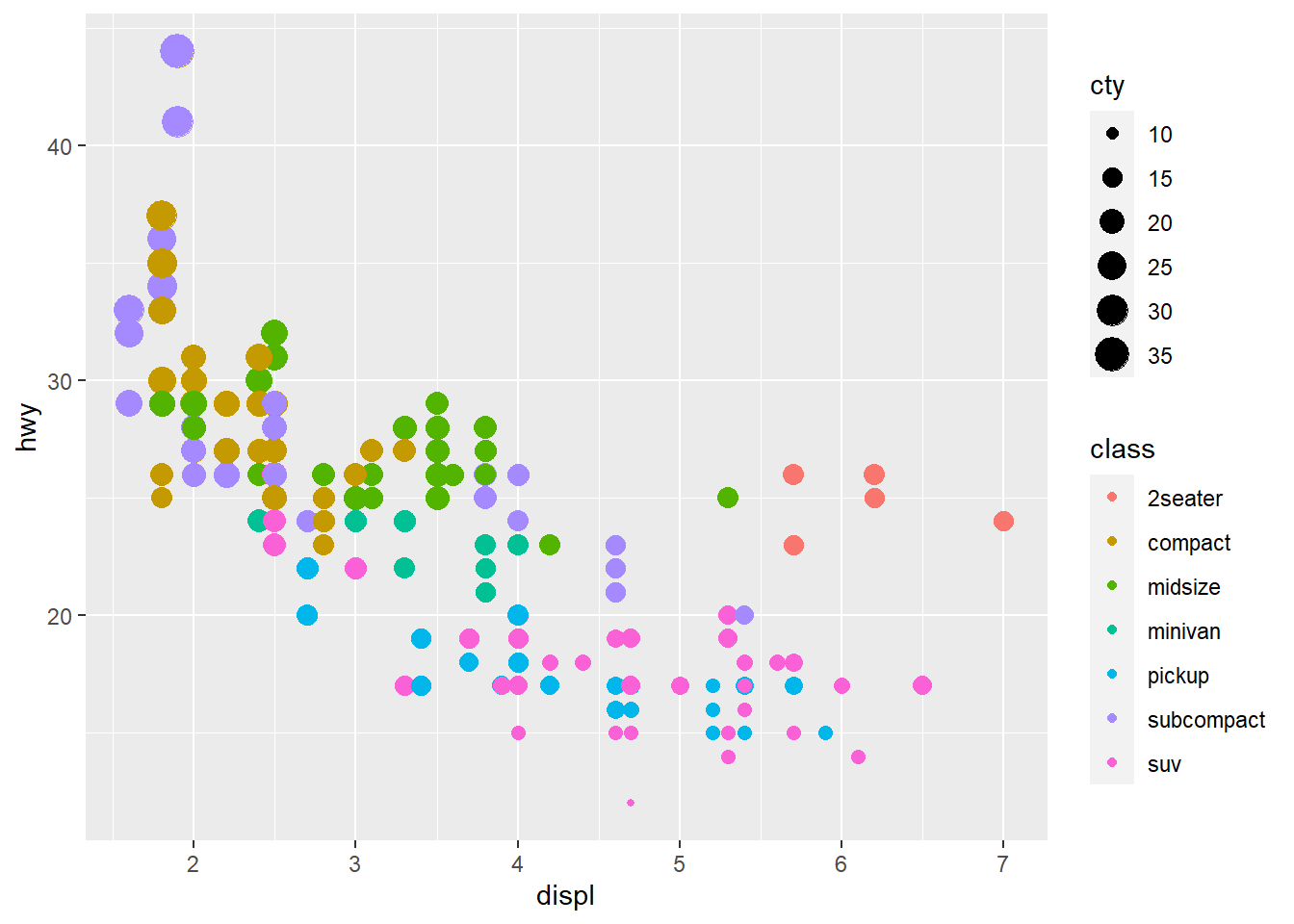
Solution:

ggplot(mpg) + 
  geom_point(aes(x = displ, y = hwy, colour = cty, size = cty))

* * *

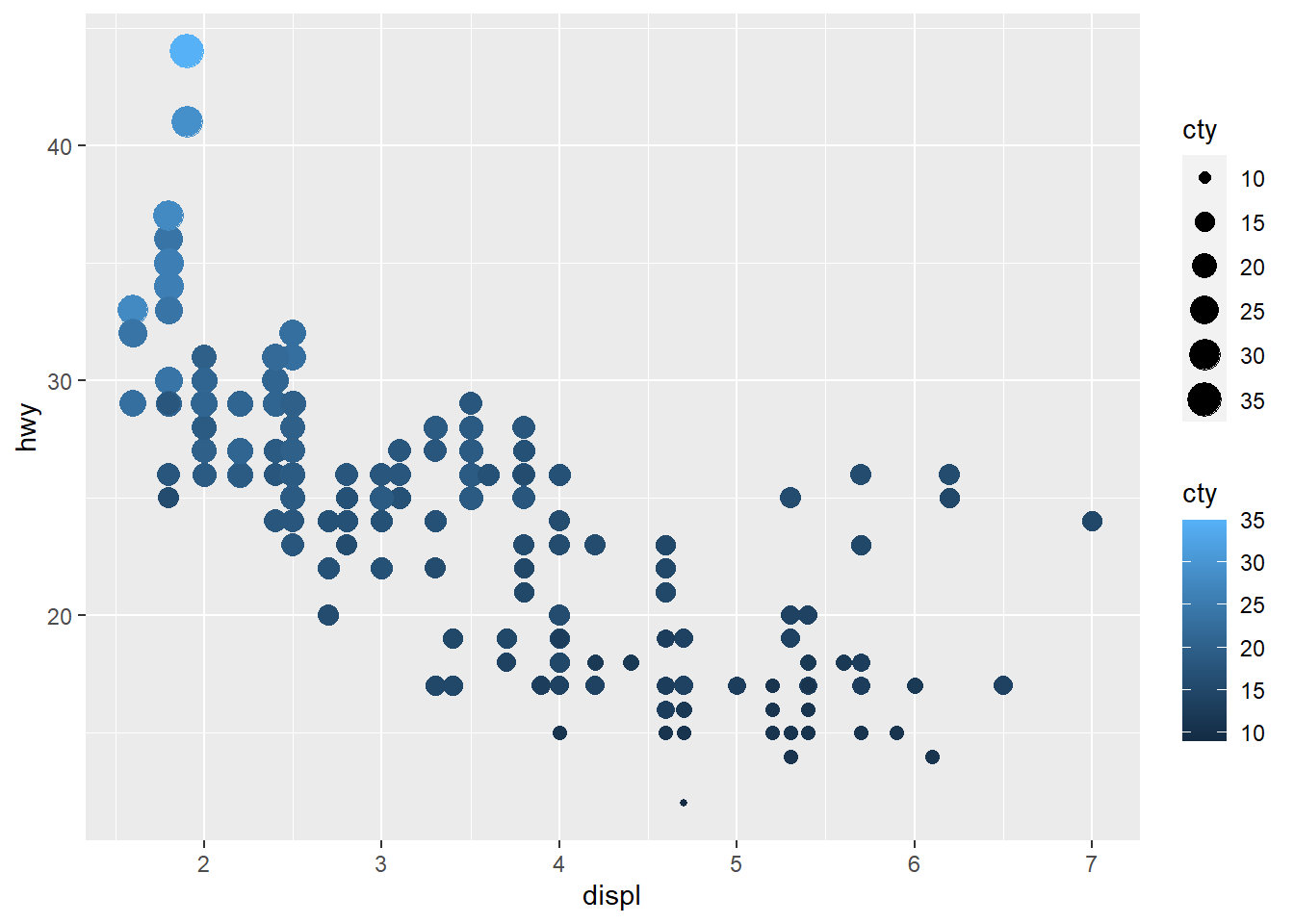The type of guide can be controlled with the guide argument in the scale, or with the guides() function. Continuous colours have a gradient colour bar by default, but setting it to legend will turn it back to the standard look. What happens when multiple aesthetics are mapped to the same variable and uses the guide type?

Solution:

ggplot(mpg) + 
  geom_point(aes(x = displ, y = hwy, colour = cty, size = cty))+
  guides(color="legend")

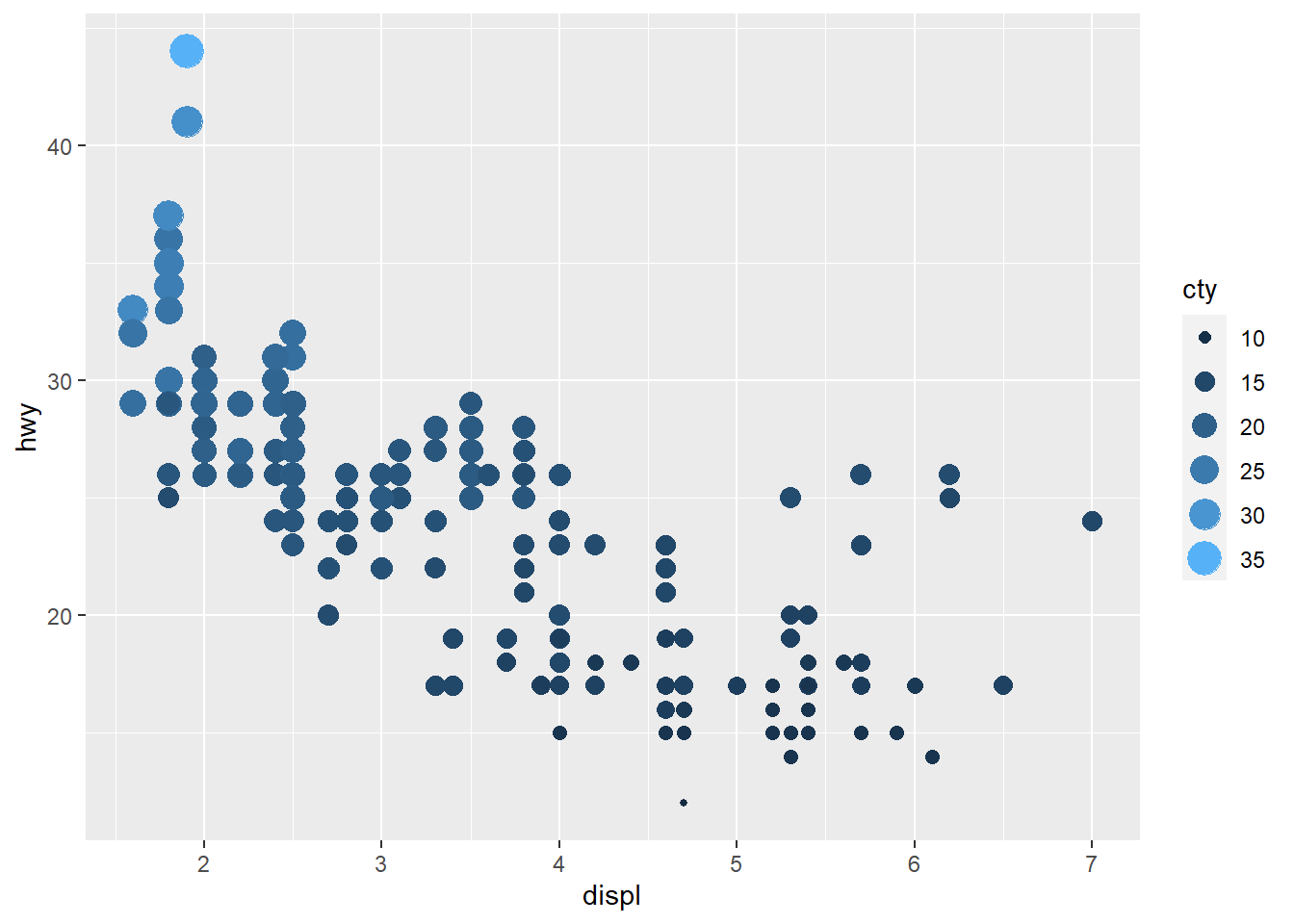ggplot combines both legends.

Facets

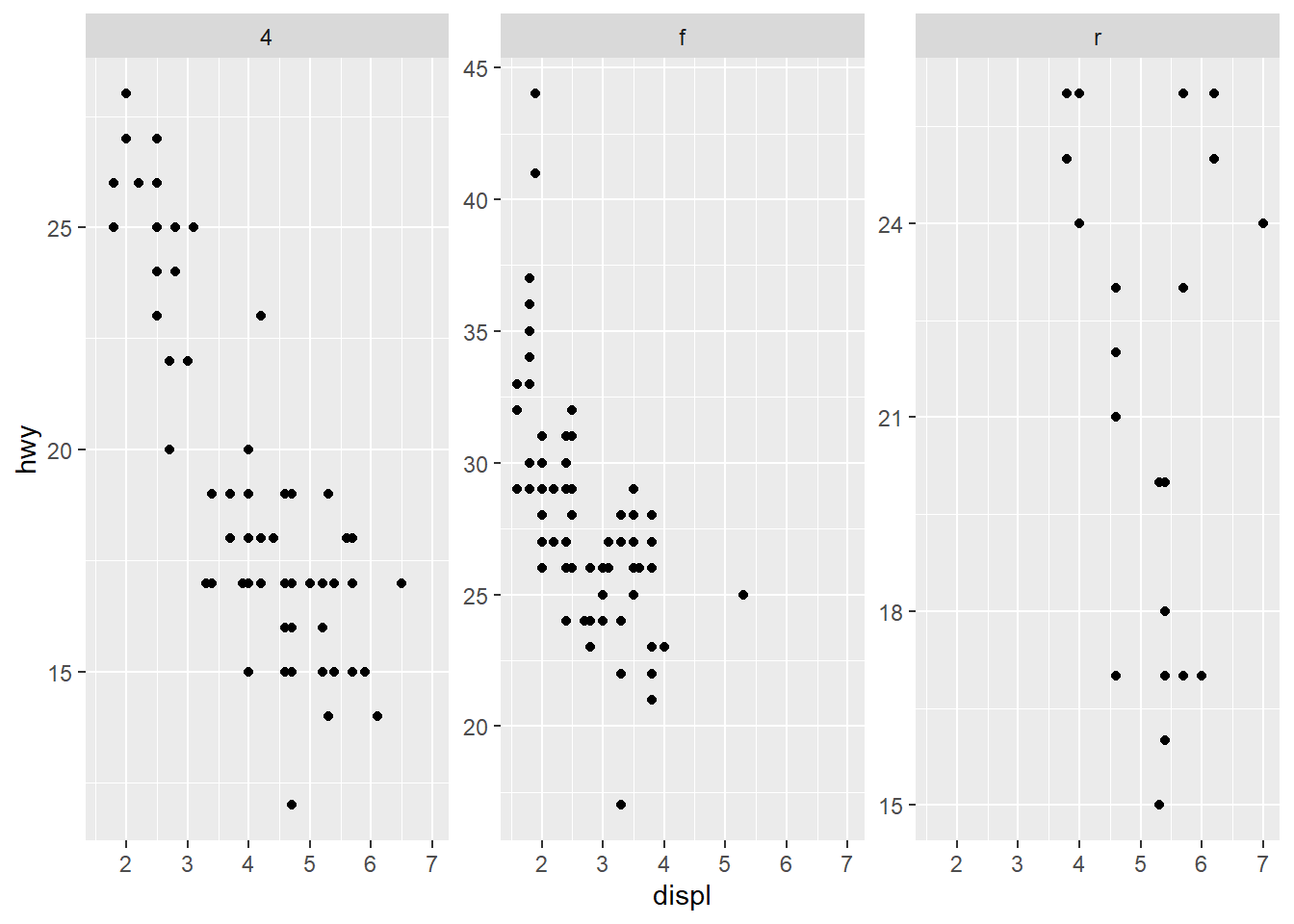
One of the great things about facets is that they share the axes between the different panels. Sometimes this is undesirable though, and the behavior can be changed with the scales argument. Experiment with the different possible settings in the plot below:

ggplot(mpg) + 
  geom_point(aes(x = displ, y = hwy)) + 
  facet_wrap(~ drv)

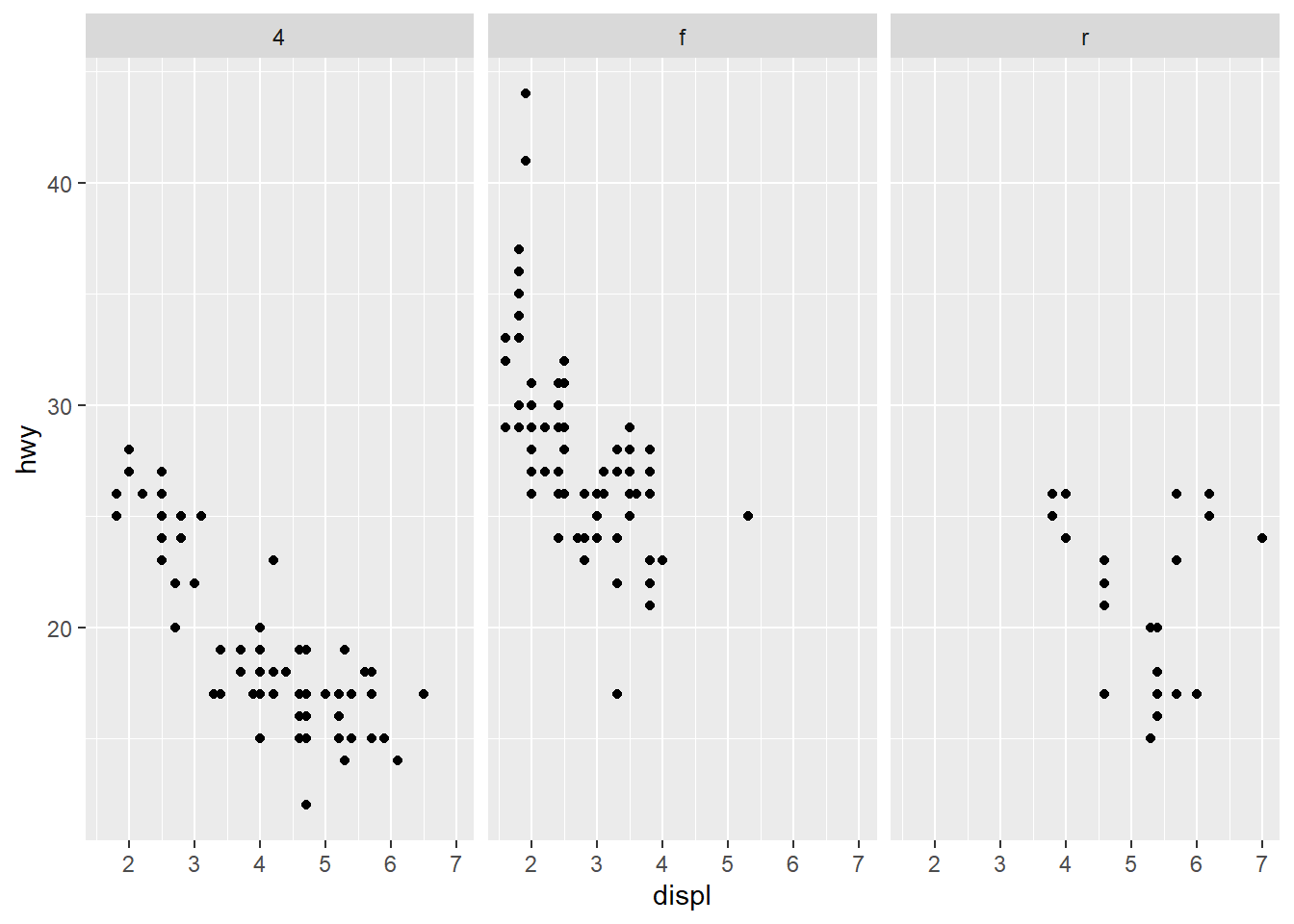
Solution:

ggplot(mpg) + 
  geom_point(aes(x = displ, y = hwy)) + 
  facet_wrap(~ drv, scales="free_y")

* * *

Usually the space occupied by each panel is equal. This can create problems when different scales are used. Can you modify the code below so that the y scale differs between the panels in the plot. What happens?

ggplot(mpg) + 
  geom_bar(aes(y = manufacturer)) + 
  facet_grid(class ~ .)

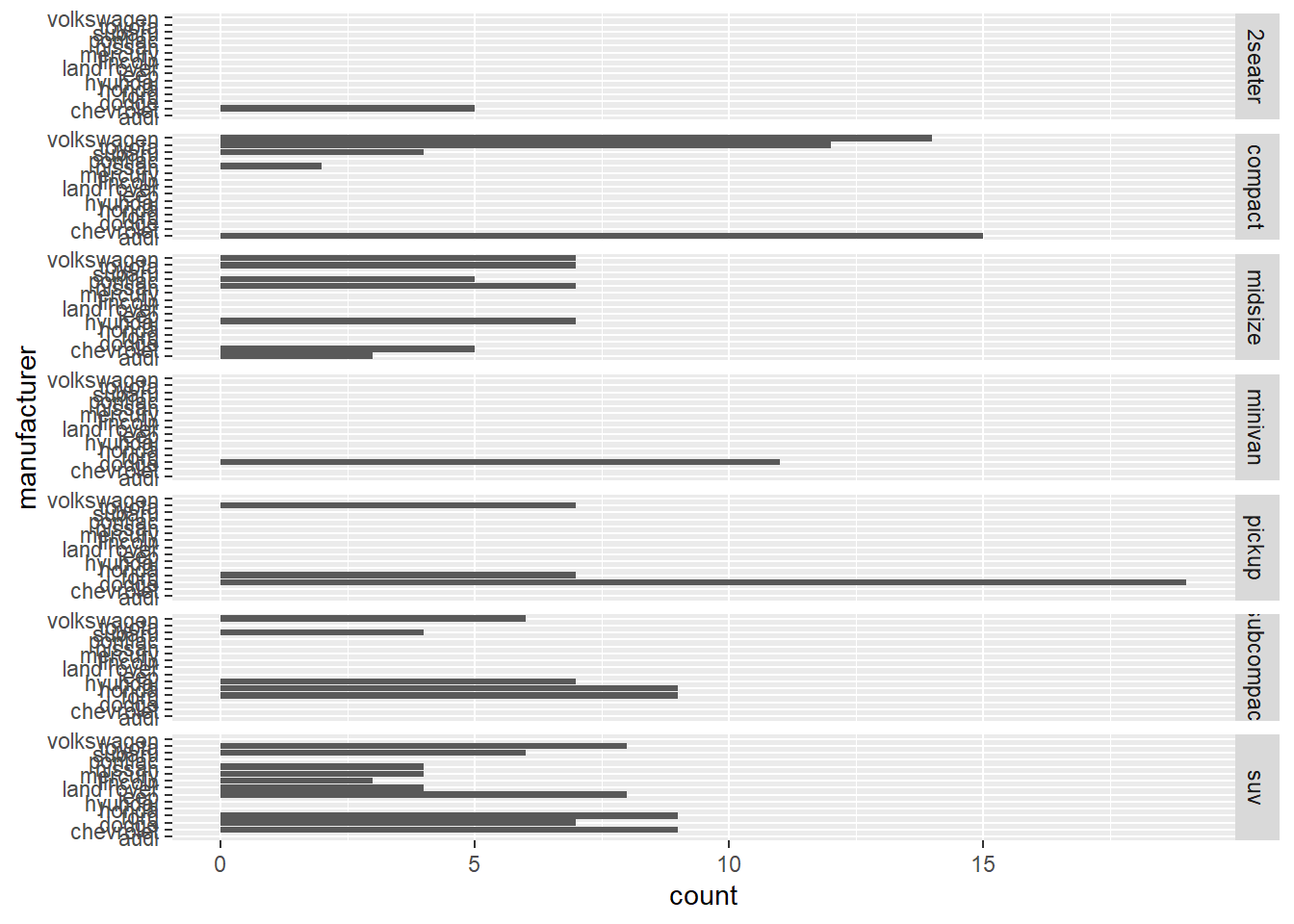
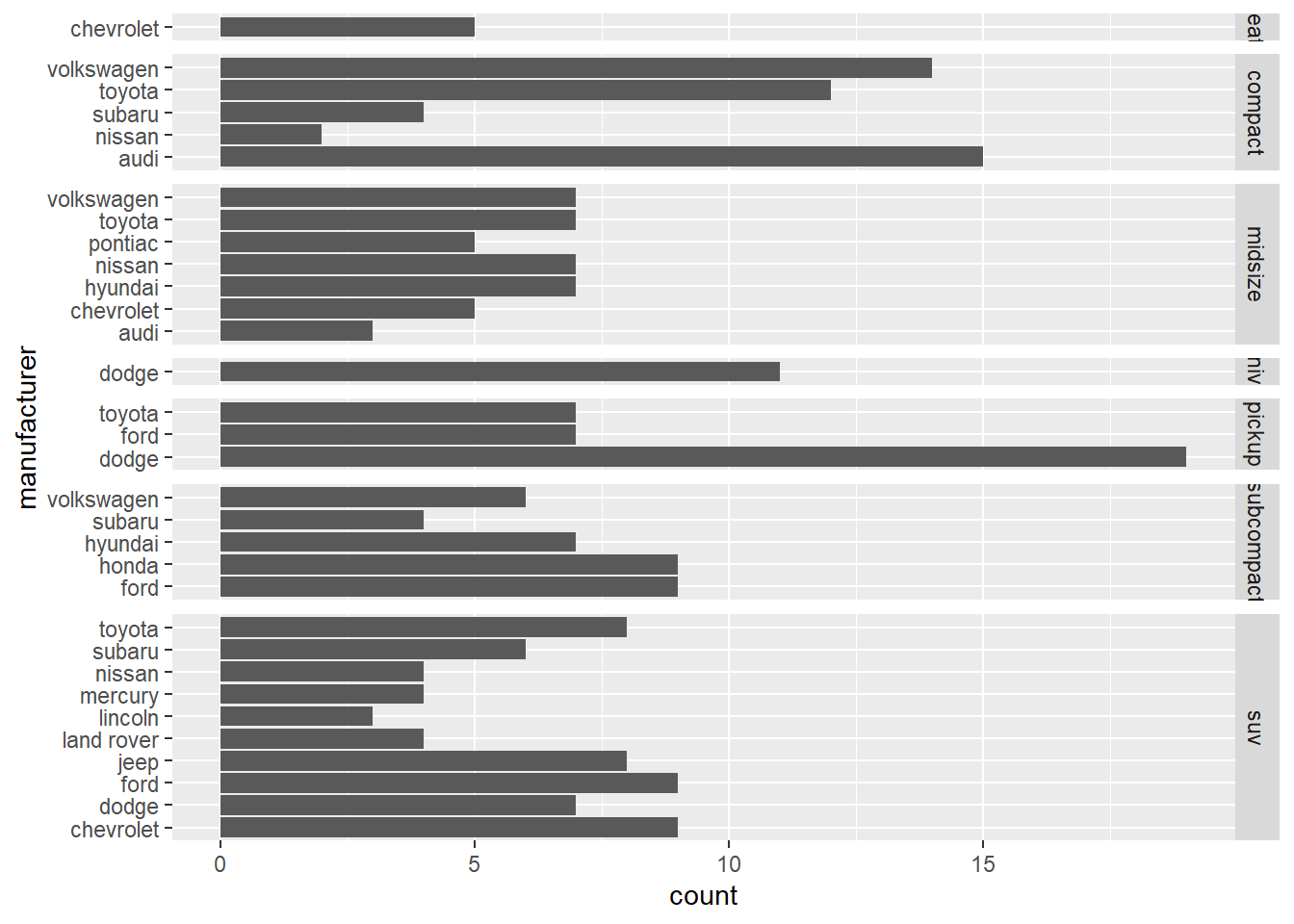
Use the space argument in facet_grid() to change the plot above so each bar has the same width again.

Solution:

data("mpg")
ggplot(mpg) + 
  geom_bar(aes(y = manufacturer)) + 
  facet_grid(class ~ ., space = "free_y", scales = "free_y")